Convolutional Graph Neural Networks with GraphSAGE – Unusually Effective

Explore how convolutional graph neural networks (CNNs) generate highly effective graph representations, particularly when leveraging the Stanford GraphSAGE framework. Also understand how CNNs can be modified for various machine learning use cases, as well as the limitations of this architecture, and how to mitigate those limitations.

Why Use a Convolutional Graph Neural Network?

As I eluded to in my previous post about graph embeddings, at the time of writing, one of the most effective methods we have for generating these embeddings is through graph neural network models. More specifically, convolutional graph neural networks which are built with a series of message passing layers or “convolutions”, such as the prevalent GraphSAGE framework.

Peeling Back the Layers of Message Passing

It has long been said, “show me your friends, and I’ll show you your future”. This old adage implies that we are not only a product of our own habits and traits but also that we are greatly influenced by those around us, a well-documented sociological phenomenon called homophily.

We can therefore think of ourselves as an amalgamation of our own nature blended with the influence of those we associate with. With that axiom, it should also hold true that those we associate with are also themselves comprised of their own nature, along with the influence of those around them, including our own influence on them as well. This example demonstrates the exact principle on which the convolutional graph neural network message passing architecture is based.

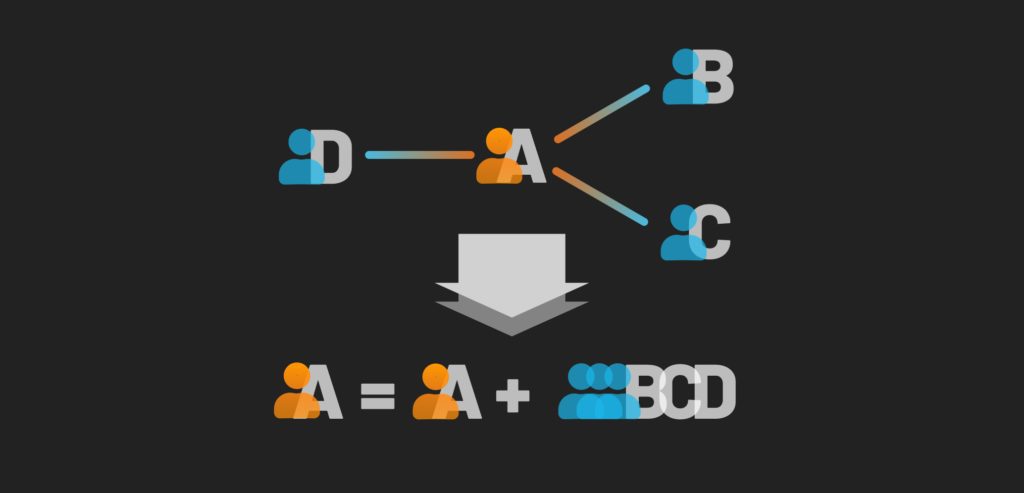
Recalling the definition in my previous post on graph embeddings, graph embeddings provide n-dimensional representations of a given node within a graph. Therefore to create a convolutional graph neural network embedding, we must first define two things:

1. What defines the similarity between two nodes?
2. How do we encode the nodes of a graph using this similarity measure?

If we define similarity based on how close two individuals are, based on the combination of their own traits and their neighbors, but also importantly on the ego network they are a part of, then our example above provides the answer to our first question. Therefore, let us explore the second question above by examining how this convolutional graph neural network architecture encodes these properties.

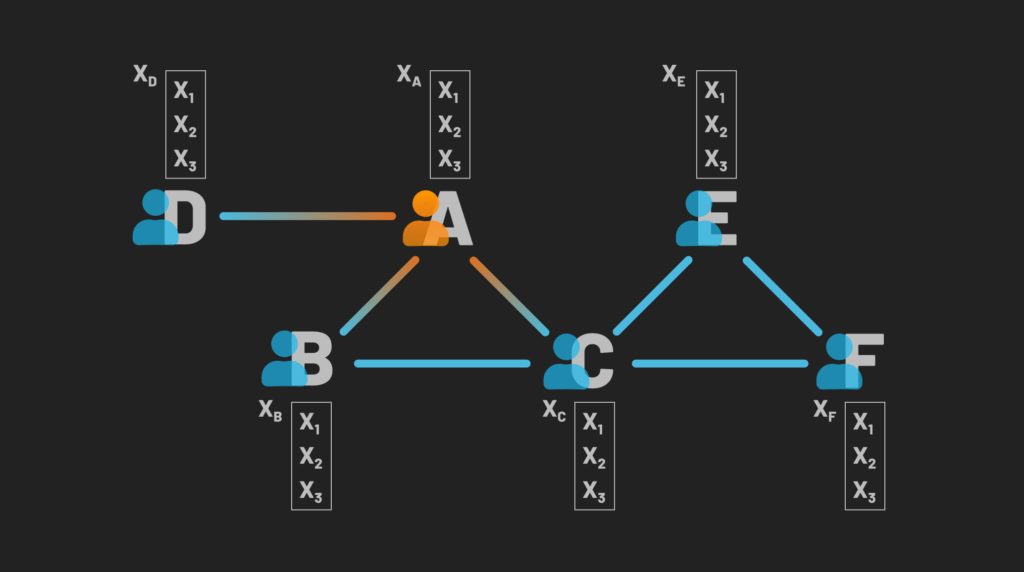
Let us imagine we have a small graph that represents a social network. Each connection within the graph represents whether or not two individuals are friends. For each node representing a person, we also have a set of properties that inform how similar they are such as age, activity level, and whether or not they have watched the TV show “Stranger Things” for this example. So we have the following:

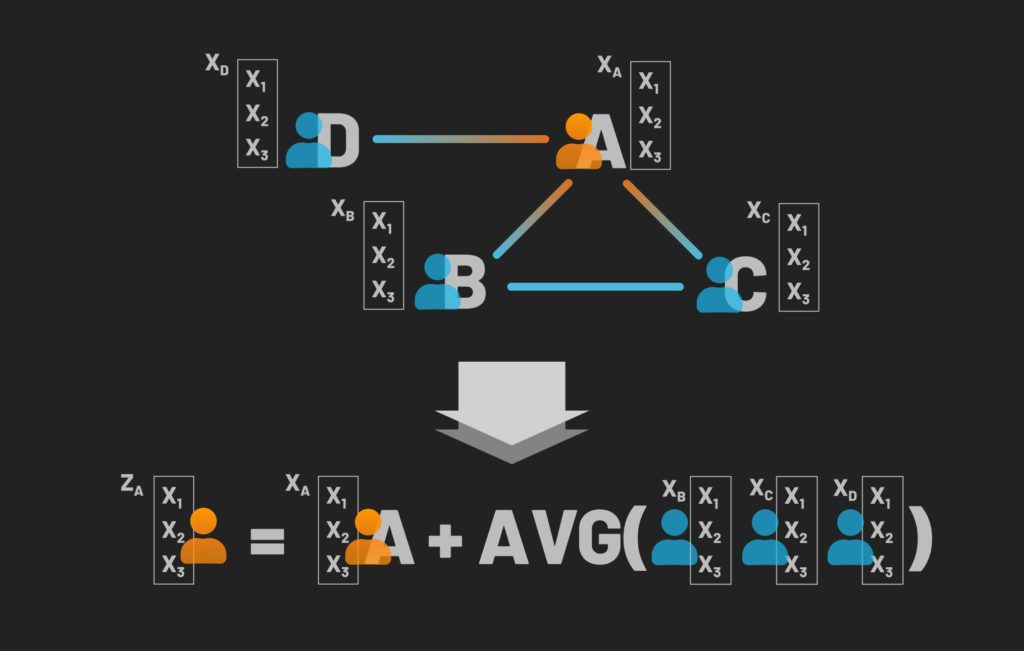
Next, to capture the influence of our neighbors we will treat the encoding of each node as a combination of its own feature-vector combined with the average feature-vectors of its neighbors.

Next, let’s extend this concept further by not only considering the neighbors who are directly connected to the node in question but also how that node’s neighbors are influenced by its own neighbors, and the extended ego network as the broader context. The depth of this “neighbor’s neighbor” influence which we consider in our embedding is defined by the hyperparameter K. In this example, we will use K=2.

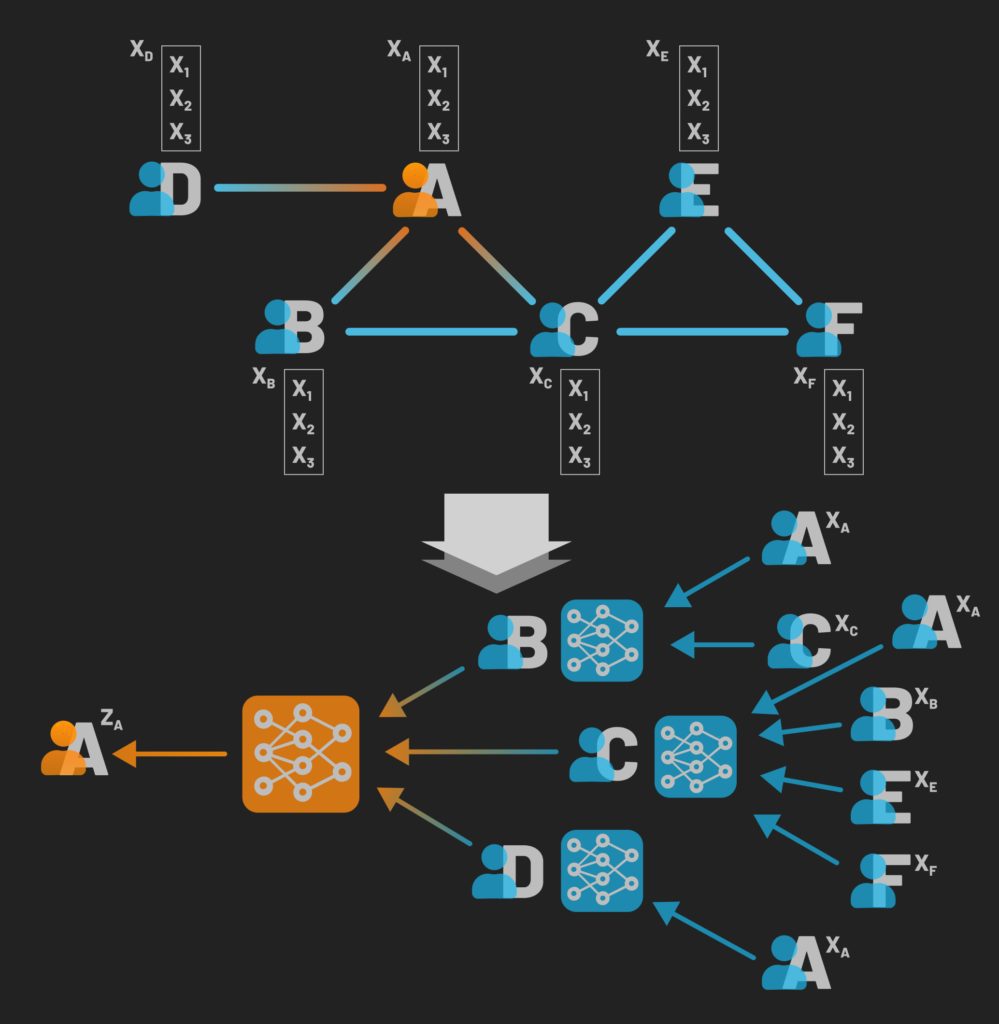
With each set of aggregations, a neural network is applied to create another layer of information which is then passed along to the next set of aggregations, essentially messaging through the connections, creating a set of convolutions, hence the name “message passing” and “convolutional graph neural network“.

Thus we can see how to represent a given node as a set of cascading aggregations of its neighbors and their neighbors. With that idea and visual in place, let’s look at this from a more concrete, mathematical viewpoint.

What is GraphSAGE?

GraphSAGE is one of many frameworks available for inductive representation learning on large graphs, but it is the most common at the moment for CNN analysis. For that reason, we use it as a means to explain how to use convolutional graph neural networks

Breaking Down GraphSAGE Encodings

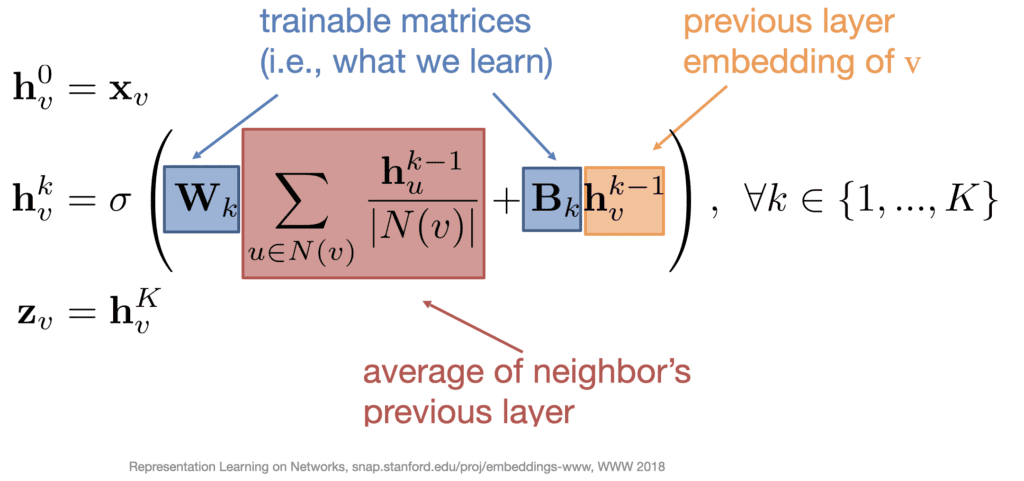
For each layer of aggregation where a neural network is applied, two sets of weight matrices are used to govern the influence of the two main components of this model – a node’s own information and the averaged information of its neighbors.

Because these weights are learned for each layer of K, this produces a total of K * 2 sets of weights in the final function. These learnable weights not only allow for improved encodings, but they also help to define a unique encoding function after training, allowing us to create embeddings for previously unseen data – otherwise known as induction.

The Inductive Advantage

Another powerful benefit of convolutional graph neural networks is the fact that rather than just generating a set of encoded vectors, the output of such methods is an encoding function that we can then apply to a given node to generate its vector representation. This contrasts against previously discussed methods such as node2Vec which is transductive in nature due to the fact that it only produces embeddings for the data on which they are trained and must be retrained as new data is introduced.

With Inductive models, we can reuse the generated encoding function for previously unseen data to generate an embedding representation of that node in the context of the rest of the existing graph. This is a powerful capability, especially since retraining a model can introduce increased computation costs.

Modifying GraphSAGE

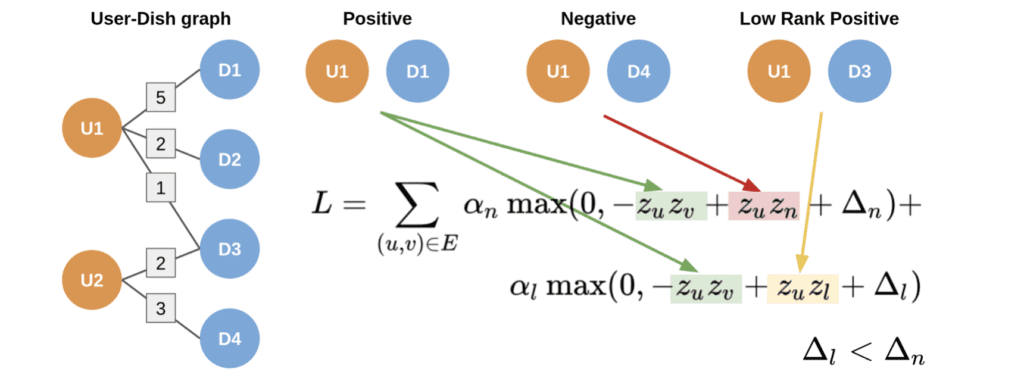
Another advantage of convolutional graph neural networks is that these embeddings can then be fed into any loss function to perform tasks such as node classification. This loss function can even be further specified to handle domain-specific nuances in the machine learning task. For example, as the Uber Eats team explains in their blog on the subject, they do not want to simply classify which dishes a user may like or dislike, they want to capture the additional subtlety between a positive dish vs a low-ranking positive dish for a user. To do this, they simply incorporated that logic into their modified loss function to handle the ordinal nature of the prediction.

Among the many advantages of customizing one’s approach with GraphSAGE is that one will have embeddings that better fit the ultimate goal of the analysis, whether it be classification, link prediction, and so on, as opposed to simply considering the similarity for example. Incidentally, this approach also has advantages when compared to using node2vec.

Limitations of Message Passing

Despite the performance of convolutional graph neural networks, their underlying architecture still presents problems that remain unaddressed within the field of geometric deep learning. One of these is the issue of distant signal compression, where the signal from one or a few distant but important nodes is drowned out by the information from closer neighbors when aggregated multiple times, across layers. This architecture implies that those closest to you provide the most information, which while often true, is not always the case for many domains.

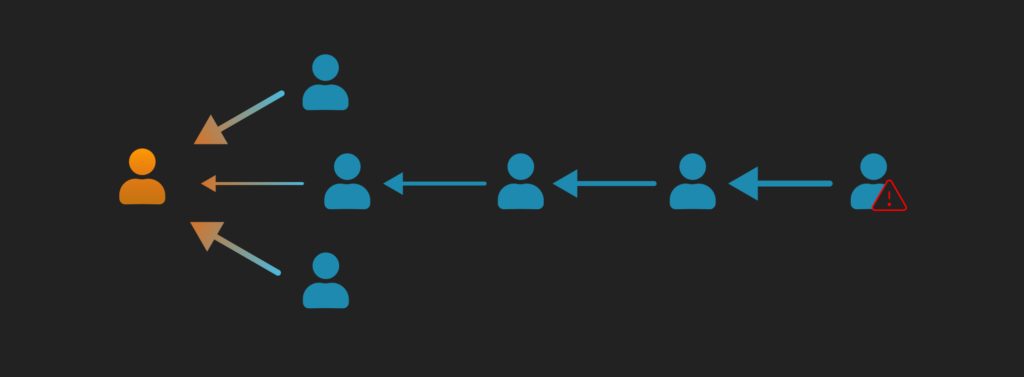
This is easily demonstrated in the case of money laundering or fraud where only one or a few nodes within a given neighborhood may actually be ones funneling money, but their distance from the target nodes means that by the time the convolutional graph neural network “passes” their signal, it had been compressed to the point where it is no longer detectable by the model. We also see this in biological pathways where a key node in a network may be many degrees removed from a target protein.

Other limitations include model performance in the context of temporal analysis, as well as the size of in-memory requirements for analysis. There are a variety of ways to mitigate these limitations including shortening paths and more that will be discussed in future articles.

Conclusion

Convolutional graph neural networks have brought the dawn of a new generation of machine learning techniques. Their versatility, flexibility, and robust architecture make them suitable for a variety of tasks. By following simple principles of how that which surrounds a component of a system, impacts that component, they are able to accurately model numerous use cases. As a valuable and promising approach, researchers also continue to asses any shortcomings in an effort to develop the next generation of convolutional graph neural networks.